Topological Image
Analysis using Persistence and Min-Max Diagrams
(c) Moo K. Chung
mkchung@wisc.edu
Department of Biostastics and Medical Infomatics
Waisman Laboratory for Brain Imaging and Behavior
University of Wisconsin-Madison
Description
July 14, 2010
We will
show how to construct persistence diagrms [1] and
min-max diagrams
[2] [3] for 1D (simulated functional signal) and 2D data (cortical
thickness). The persistence and min-max diagrams are motivated by
topological data analysis where the underlying topology of data and
images is quantied.
The
codes
have been tested
under a Macbook pro with 4GB
memory and MATLAB 7.5. If
you are using the Matlab codes below for your publication,
please reference [1] or [2]. The detailed description of cortical
thickness data is given in [6].
Persistence & Min-Max diagrams for 1D functions
July 14, 2010
The
construction for the persistence diagrm for 1D function is based on the
iterative
pairing and deleation algorithm [2]. Note that the min-max
diagram [2] and the persistence diagram [1] are identical for 1D
functions since there is no saddle points in 1D functions. Let us
explain 1D example given in the MICCAI 2009 paper [2]. In the interval
[0, 1], we construct a signal s and add
noise e to obtain
simulated signal Y.
x=[0:0.002:1]';
s= x + 7*(x -
0.5).^2 + cos(8*pi*x)/2;
e=normrnd(0,0.2,length(x),1);
Y=s+e;
figure;
plot(x,Y,'ko','MarkerEdgeColor',[0.5
0.5
0.5],
'MarkerFaceColor',[0.7
0.7
0.7], 'MarkerSize',4)
This produces a scatter points
so we can't obtain critical values directly. We smooth out the scatter
plot using heat
kernel
smoothing with bandwidth 0.0001 and cosine series
expansion upto degree 100 [2] [3]. The resulting smoothed signal is
stored in the variable wfs.
k=100;
sigma=0.0001;
[wfs, beta]=WFS_COS(Y,x,k,sigma);
hold on;
plot(x,wfs,'k','LineWidth',5);
Then using the
iterative pairing and deleation
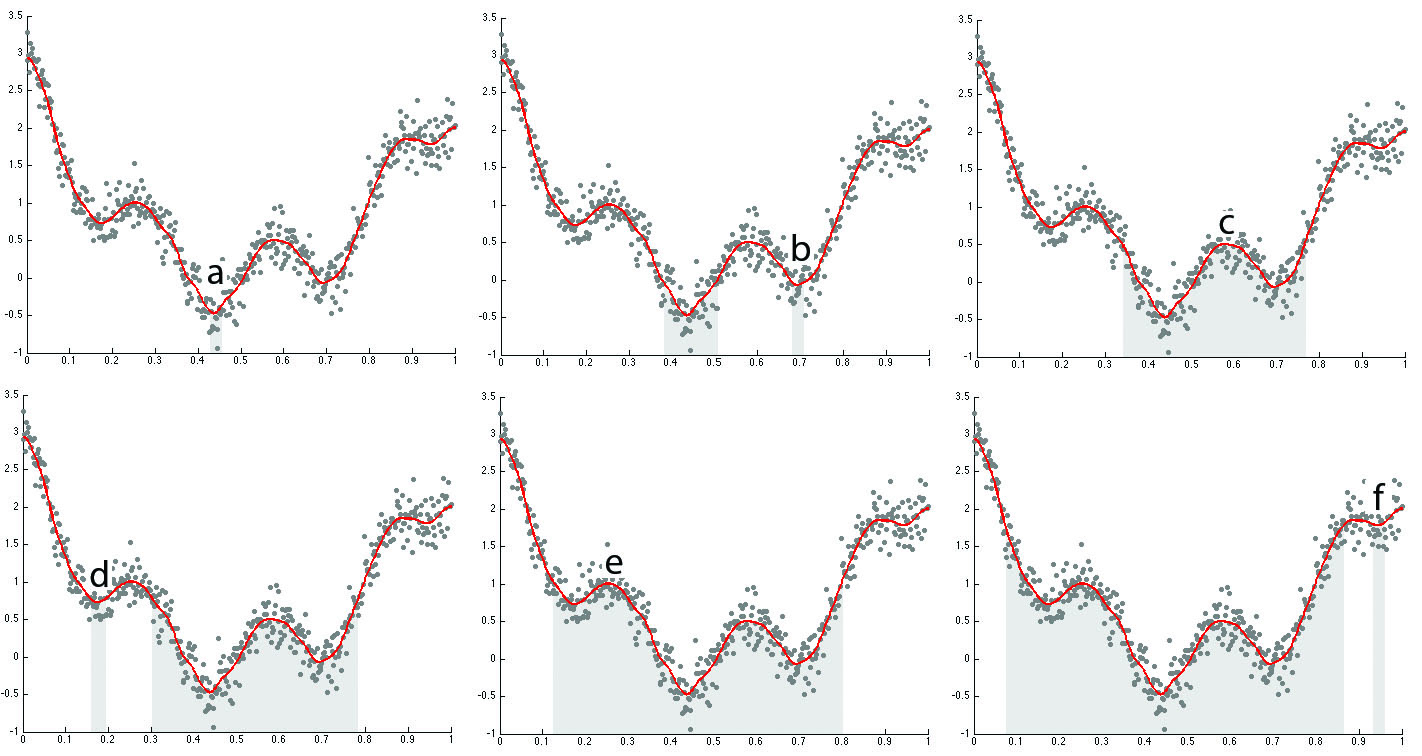
algorithm pairing_1D, we determine the pairing of
minimums and maximums. pairing_1D also plots critical values as white
dots (Figure 1).
pairs=pairing_1D(x,wfs);
set(gcf,'Color','w')
This produces 3 pairs:
>>
pairs
pairs =
1.3126 1.6816
0.5948 1.1636
0.2130 0.8886
The
result
will
be
slightly
different each time you run the code since the
added noise is always changing. The pairing rule is explained in Figure
1.
Cortical thickness data
July 17, 2010
We will
use the cortical surface data set used in [2]. There are total 16
autistic and 11 control subjects. Cortical thickness is computed as the
L2 distance between the two surfaces. autism_coord
is the gray matter surface for autistic subjects and autism_coordw
is the white matter surface for control subjects.
load AUTISM.coordinates.mat
thick_au=squeeze(sqrt(sum((autism_coord-autism_coordw).^2,2)));
thick_co=squeeze(sqrt(sum((control_coord-control_coordw).^2,2)));
We will display cortical thickness of the 1st autistic subject on a
unit sphere.
load unitsphere.mat
figure_trimesh(sphere,thick_au(1,:),
'rwb')
Since the cortical thickness data is fairly noisy, we will smooth using
the weighted-sphearicl
harmonic
representation with degree 42 and bandwidth 0.001 [4]
[5]. The detailed explanation of SPHARMsmooth is given here.
The smoothed cortical thickness is given in Figure 2.
directory='/basis/';
SPHARMconstruct(directory,42);
L=42;
sigma=0.001;
coord_co=zeros(11,3,40962);
coord_co(:,1,:)=thick_co;
[coord_sm_co,fourier_coeff_co]=
SPHARMsmooth(coord_co,L,sigma);
coord_au=zeros(16,3,40962);
coord_au(:,1,:)=thick_au;
[coord_sm_au,fourier_coeff_au]=
SPHARMsmooth(coord_au,L,sigma);
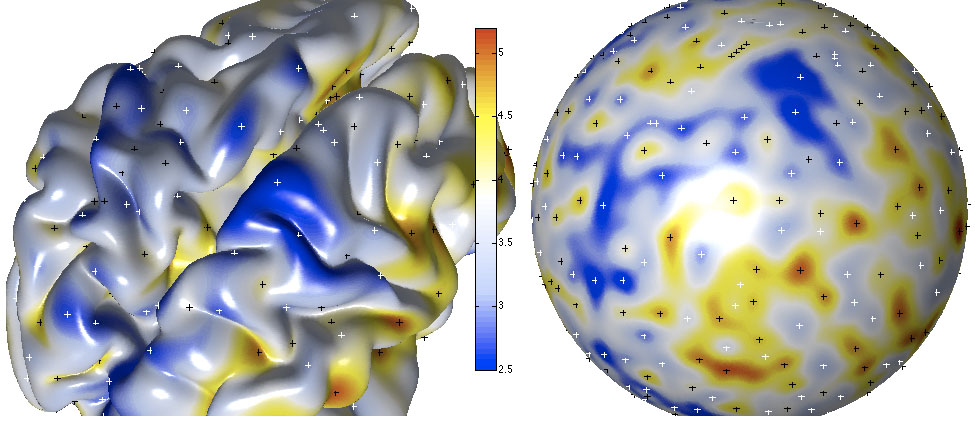
Figure 2.
Weighted spherical harmonic representation of cortical thickness.
Critical values are identified as crosses.
Min-max diagram of a function on a sphere
April 28, 2010
The
min-max diagram is constructed by pairing minimums and maximums in a
particular fashion [2]. To simplify the problem, we identify how
critical values are connected using the Delaunay triangulation.
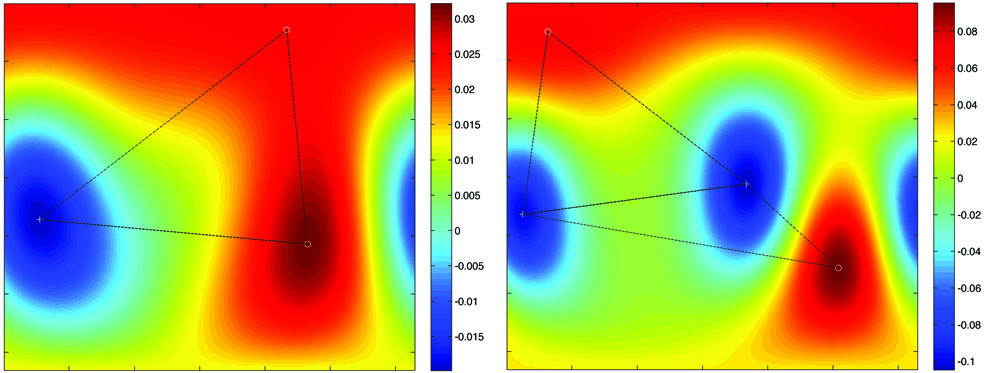
Figure 3.
Delaunay triangulation of few minimums and maximums.
Let us map
cortical thickness given in Figure 2 onto a plane for better
visualization. fourier_coeff_au.x(:,:,1)is the spherical harmonic
coefficients of the 1st autistic subject.
square=SPHARM2square(fourier_coeff_au.x(:,:,1),42,0.001);
[lmax,
lmin]
= figure_extrema(square);
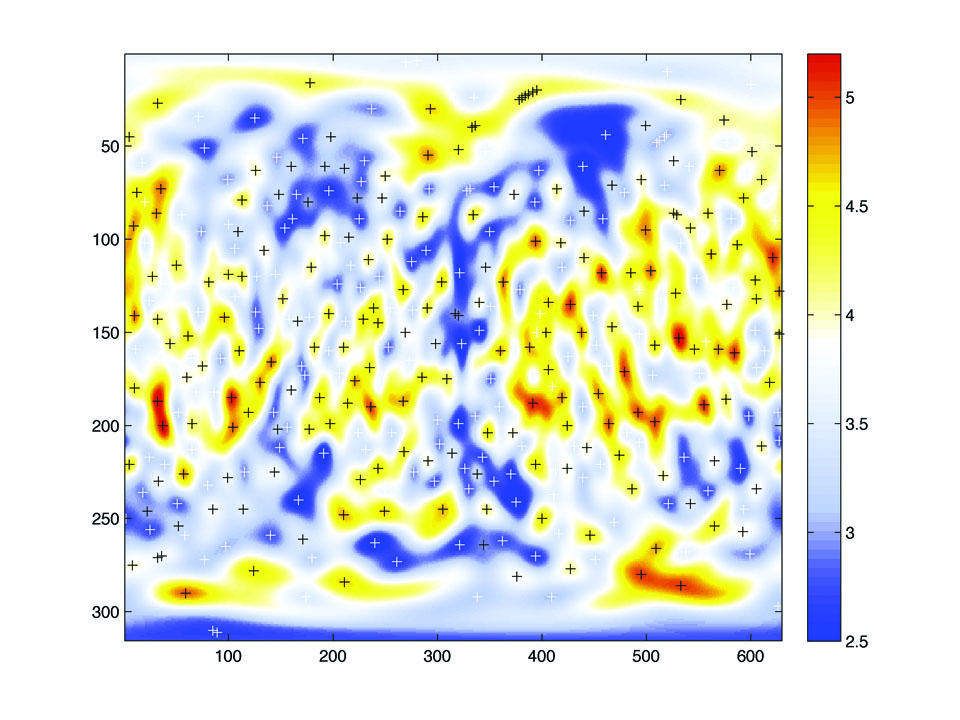
Figure 4. Flatmap represention of cortical thickness given in
Figure 2. Critical values are identified as crosses.
The minimum and maximums in the cortical thickness data are paired
using the
iterative
pairing and deleation algorithm [2]. The pairing for all
critical values identified in Figure 2 and 4 can be done by
value=squeeze(coord_au(1,1,:));
pairs= pairing_mesh(sphere, value, L,
sigma);
The code requires FINDnbr.
Since
we
are expected to obtain topologically invariant pairing, we
constructed the pairing in the spherical mesh.
References
April
22,
2010;
October 8, 2010
- Chung, M.K., Bubenik, P.,
Kim, P.T.
2009. Persistence
diagrams
of
cortical
surface
data. Information
Processing
in Medica Imaging
(IPMI). Lecture Notes in
Computer Science (LNCS). 5636:386-397.
- Chung, M.K., Singh, V., Kim,
P.T., Dalton, K.M., Davidson, R.J.
2009. Topological
characterization
of
signal
in
brain
images
using
the
min-max
diagram. 12th
International
Conference on
Medical Image Computing and Computer Assisted Intervention (MICCAI).
Lecture Notes in Computer
Science
(LNCS). 5762:158-166.
- Pachauri, D., Hinrichs, C., Chung, M.K., Johnson, S.C., Singh, V.
and ADNI. 2010. Cortical surface topology based kernels with
application to alzheimer's disease. IEEE
Transactions
on
Medical
Imaging.
under revision.
- Chung, M.K., Dalton, K.M., Davidson, R.J. 2008. Tensor-based
cortical
surface morphometry via weighed spherical harmonic
representation. IEEE Transactions on Medical Imaging. 27:1143-1151.
- Chung, M.K., Dalton, K.M., Shen, L., L., Evans, A.C., Davidson,
R.J. 2007. Weighted
Fourier series representation and its application
to quantifying the amount of gray matter. IEEE
Transactions on Medical Imaging 26:566-581.
- Chung, M.K., Robbins,S., Dalton, K.M., Davidson, Alexander, A.L.,
R.J., Evans, A.C. 2005. Cortical
thickness analysis in autism via heat kernel smoothing. NeuroImage 25:1256-1265



