
Figure 1. Left hippocampus showing possible mesh noise.
Description
April 24, 2010; July 16, 2011
The concept of heat kernel
smoothing along an arbitary manifold has been first
introduced in 2005 [3][4]. The Gaussian kernel weights
observations according to their Euclidean distance. When
the observations lie on a convoluted brain surface and
arbitary manifolds; however, it is more natural to assign
the weight based on the geodesic distance along the
manifolds. On the curved manifold, a straight line between
two points is not the shortest distance so one may
incorrectly assign less weights to closer observations.
Therefore, smoothing data residing on manifolds requires
constructing a kernel that is isotropic along the geodesic
curves.
The original implemenation
given in [3][4] was fomulated as iterated kernel
convolutions that approximate Gaussian kernel smoothing in
the tangent space locally. The MATLAB code is given in http://www.stat.wisc.edu/~mchung/softwares/hk/hk.html.
To correct for the confounding numerical error over each
iteration, we introduced a new smoothing framework that
uses the eigenfunctions of the Laplace Beltrami operator.
This implementation of heat kernel smoothing probably
solves an isosotropic heat diffusion on the manifolds mos
accruately without the problem of divergence. Our new
method performs surface data smoothing by
constructing the series expansion of the eigenfunctions of
the Laplace-Beltrami operator [6][7]. This new analytic
framework improves upon the previous iterated kernel
smoothing fomulation [3] [4] with improved numerical
accuracy and stability. The
codes have been tested on an old Mac computer (intel processor) with 4GB
memory and MATLAB 7.5, and 2.66Ghz Quad-Core
Intel Xeon Mac computer with 32GB and MATLAB 7.9. If you are using the Matlab codes/sample
data below for your publication, please reference [6]
or [7], which introdued the method given here. This is
the only publically available MATLAB code out there.
Hippocampus
Surface Data
April 22,
2010
hipporight =
vertices: [2312x3 double]
faces: [4620x3 double]
figure;figure_patch(hippoleft,[0.7
0.7 0.6],0.5)

Figure 1. Left hippocampus
showing possible mesh noise.
Eigenfunctions
of Laplace-Beltrami Operator
April 22,
2010; July 1, 2011
The concept
of heat kernel smoothing in
manifolds was originally given in [3] [4]. The original
implemenation was based on the iterated linear approximation
of the heat kernel using a Gaussian kernel in the tangent
space, which componds error when the number of iterations
increase. FreeSurfer package is also based on a similar
iterated Gaussian kernel smoothing. Our new
Laplace-Beltraim eigenfunction approach uses the
eigenfunctions of the Laplace-Beltrami operator in
representing the heat kernel as a series expansion involing
the eigenfunctions [6] [7].
To smooth
left hippocampus surface, with sigma = 0.2 and 2000
eigenfunctions, we run
hippolefts
= lb_smooth([],hippoleft, 0.2,
500, V, D);
The
first argument is where input signal should go but since the
surface coordinates themselves are signal, we do not need to put
input signal.
figure; figure_patch(hippolefts,[0.7
0.7 0.6],0.5);
-0.0000
2.0007
2.0007
2.0007
6.0044
6.0044
6.0044
6.0044
6.0044
....
Heat
kernel Smoothing in 2D images: analytic construction of
scale-spaces
November 22, 2011
We
will show you how to construct the scale-space representation of
2D images analytically via heat kernel smoothing. The
Laplace-Beltrami eigenfunctions in the Euclidean space is simply
given in terms of the product of sine and cosine functions. We
first estimate the Fourier coefficients corresponding to the basis
functions. Then we only need to change the bandwith of haet kernel
in the computation to have another scale-space. This is an
extremely powerful framework not often used since it used to be
computationally demanding.
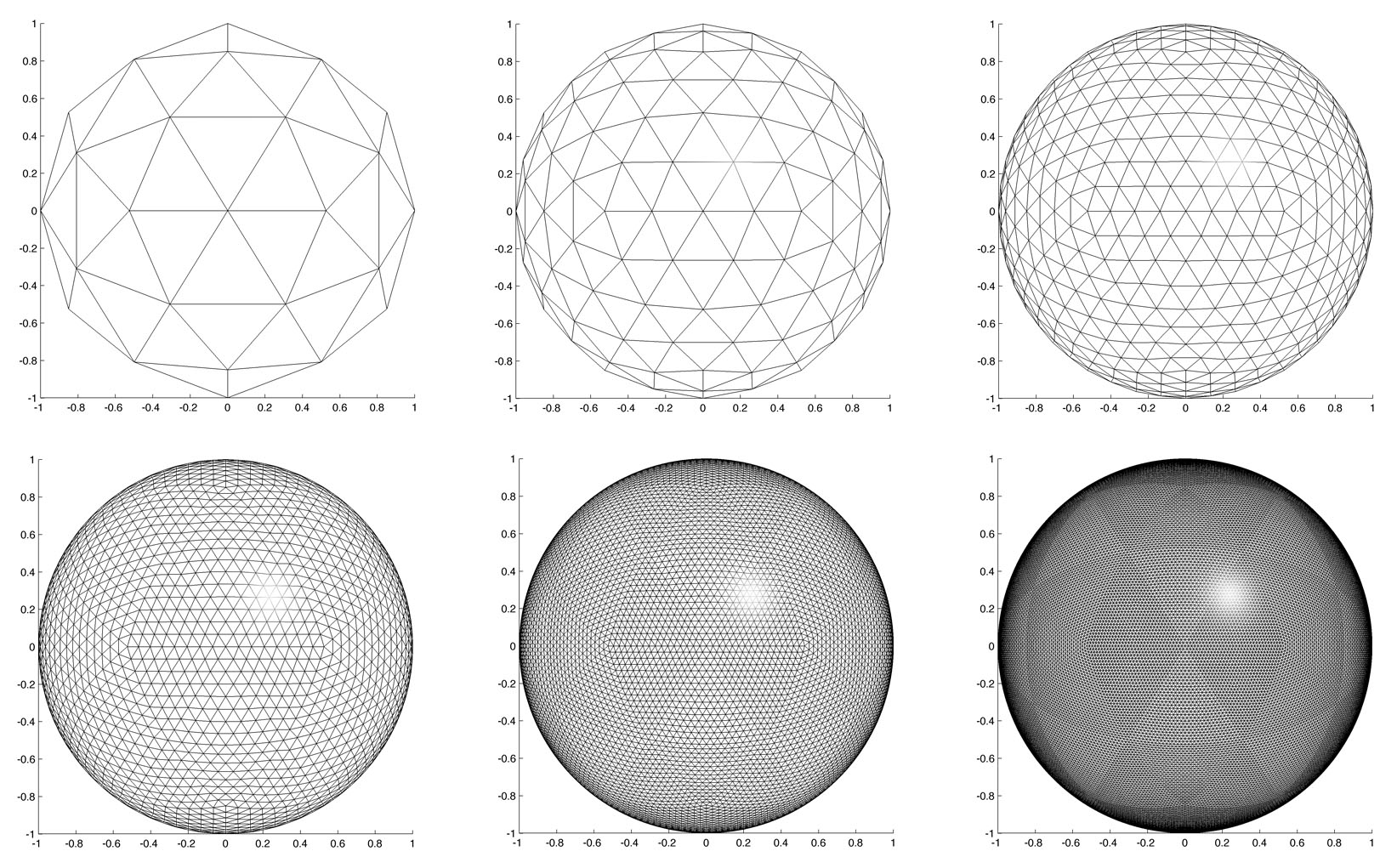
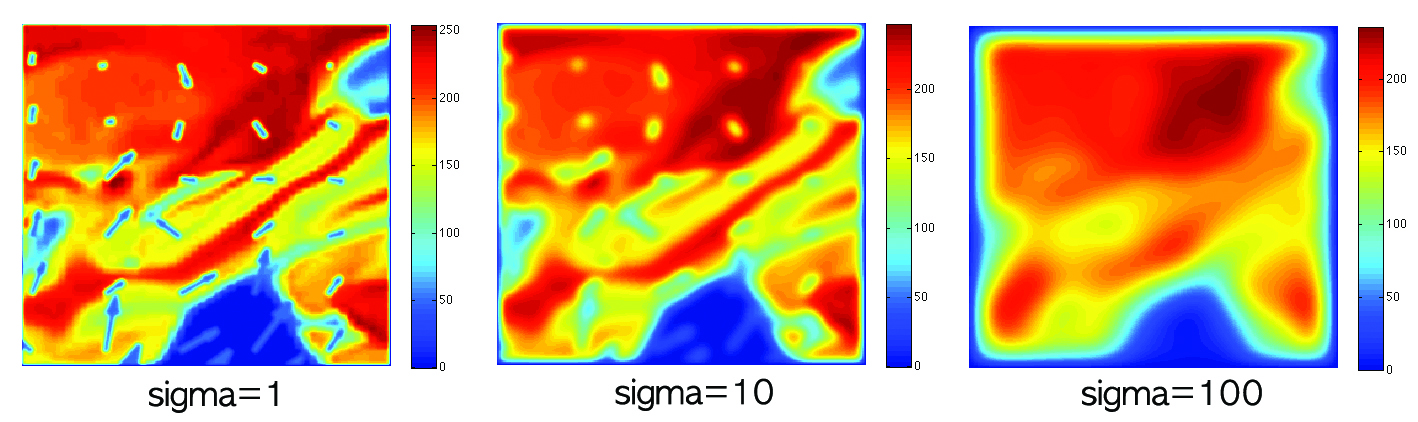
In 2D
rectangle of size of size 300 x 300, eigenfunction_box will
construct the eigenfunction of degree l in the box size L (Figure
5).
References
April 22, 2010