Structural brain
network construction using ε-neighbor method
(c) Moo K. Chung, Nagesh Aldur mkchung@wisc.edu
Department of Biostastics and Medical Infomatics
Waisman Laboratory for Brain Imaging and Behavior
University of Wisconsin-Madison
Description
April 24, 2010
Based
on
the ε-neighbor
algorithm
[1] [2],
the
brain connectivity of DTI fibers can be obtained as an
adjacency
matrix.
The algorithm was first introduced in OHBM [1] then
refiend in [2]. [3] performs the ε-neighbor network consruction on a
template so the resulting networks have identical node
positions in the template. [4] modfied the
ε-neighbor
method to be applicable to arbitrary connectivty matrix. Here
we present the ε-neighbor
algorithm and visualization and analysis tools.
The
codes
have been tested
under
Matlab versions 7.5 on a Mac computer (intel processor)
with 4GB
memory and MATLAB 7.5.
If
you are using the Matlab codes/sample data given here
for your publication,
please reference [2].
Fiber bundle visualization
July 7, 2010
Let's
load
the FA map of the template used in [1] [2]. We have to
swap x- and
y-coordinates since the MATLAB convention is slightly
different from
the usual NII-format. You need to unzip nii.zip
file from the link below.
nii=load_nii('mean_diffeomorphic_initial6_fa.nii');
d=nii.img;
surf =
isosurface(d);
coord=surf.vertices;
temp=coord;
temp(:,2)=coord(:,1);
temp(:,1)=coord(:,2);
surf.vertices=temp;
figure_patch(surf,[0.74 0.71
0.61],0.2);
hold on;
We will superimpose white matter fiber bundles on top of the FA-map.
SL.mat
contains information about 10000 tracts stored as cell data
structure.
To extract coordinates of the i-th tract, call SL{i}.
load
SL.mat
for
i=1:30:10000 % subsampling 1 for every 30 tracts
tract=SL{i}';
if
size(tract,2)>
10
hold
on
plot3(tract(1,:),tract(2,:),tract(3,:),'b')
end;
end;
To
obtain
the
two end points of tracts and color them as read,
we run
endp=get_endp_tracts(SL,30);
hold on;
plot3(endp(:,1,1),endp(:,1,2), endp(:,1,3),'.r')
hold on;
plot3(endp(:,2,1),endp(:,2,2), endp(:,2,3),'.r')
The resulting image is shown in Figure 1.
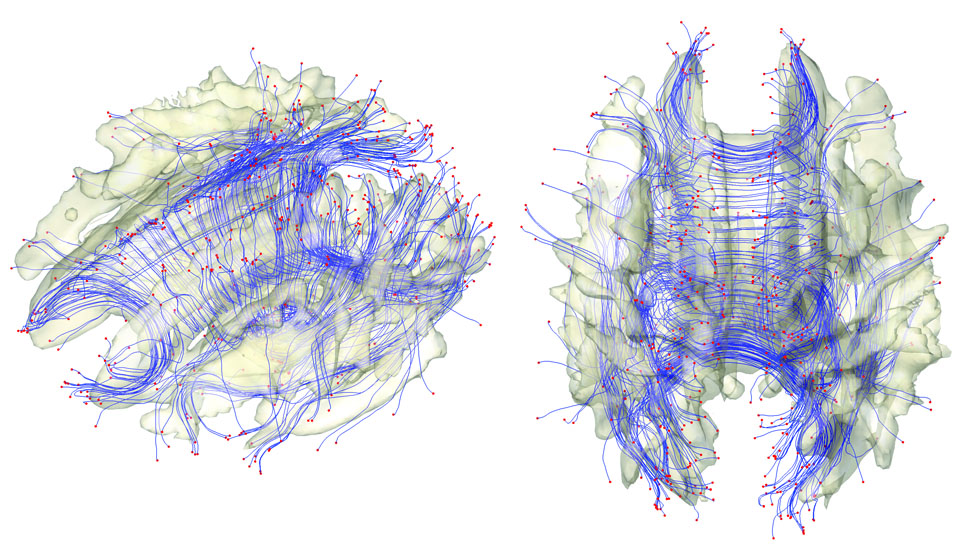
Figure 1. White matter fiber bundles obtained from a
streamline-based
algorithm. The tracts are sparsely subsampled for better
visualization.
The end points are colored as red. The surface is the
isosurface of the
template FA map so some tracts are expected to be
outside of the
surface. The ε-neighbor
method
will use the proximity of the ends points in
constructing the
network graph.
ε-neighbor algorithm
July 7, 2010
The
ε-neighbor algorithm is run directly on
the list of
fiber bundles SL.mat.
adj
is the adjacency matrix, prob
is the fiber concentration density, which is computed by
counting the
number of tracts that is connecting to the given node within
ε-neighbor. vertices
is the coordinates of the constructed nodes. Figure 2 shows
the
resulting graphs superimposed on top of the FA template and
the
corresponding adjacency matrices.
[adj,
prob,
vertices]=tract2graph(SL,10);
figure; imagesc(-adj); colormap('bone');
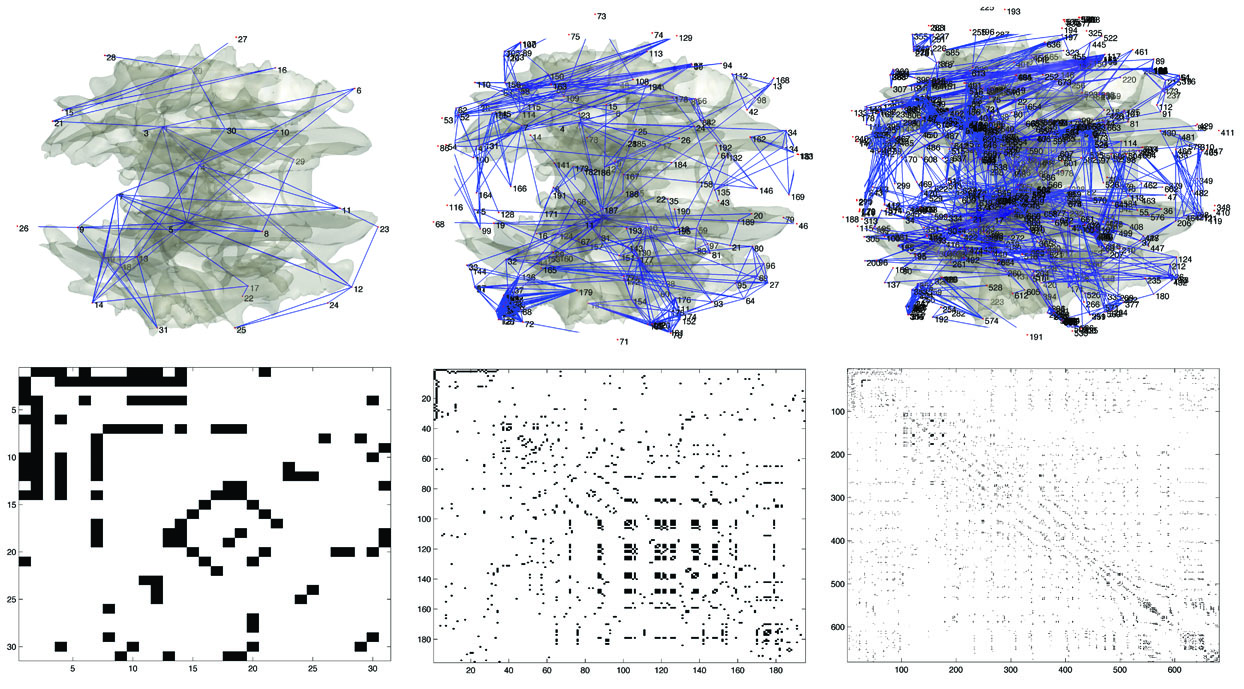
Figure 2. Scalable 3D connectivity graphs constructed from the
proposed
algorithm and the corresponding adjacency matrices. The nodes are
indexed by numbers. From the left to right, graphs are at 20, 10
and
6mm resolution.
3D
graph display
April 28,
2010
Download a sample data dtigraph.mat
that contains the
adjacency matrix adj
consisting of zeros and ones, and vertices
that contain the coordiantes of nodes.
load dtigraph.mat;
To
compute
the
degree of nodes, we sum the adjaceny matrix either along
the row or the column direction. The node degree can be displayed in
3D:
degree=sum(adj);
figure_graph_color(adj,vertices,degree+0.001);
colormap('hot');
The number 0.001 is added to avoid an error associted with
using the default MATLAB command scatter3
that can't drow a ball of 0 radius.
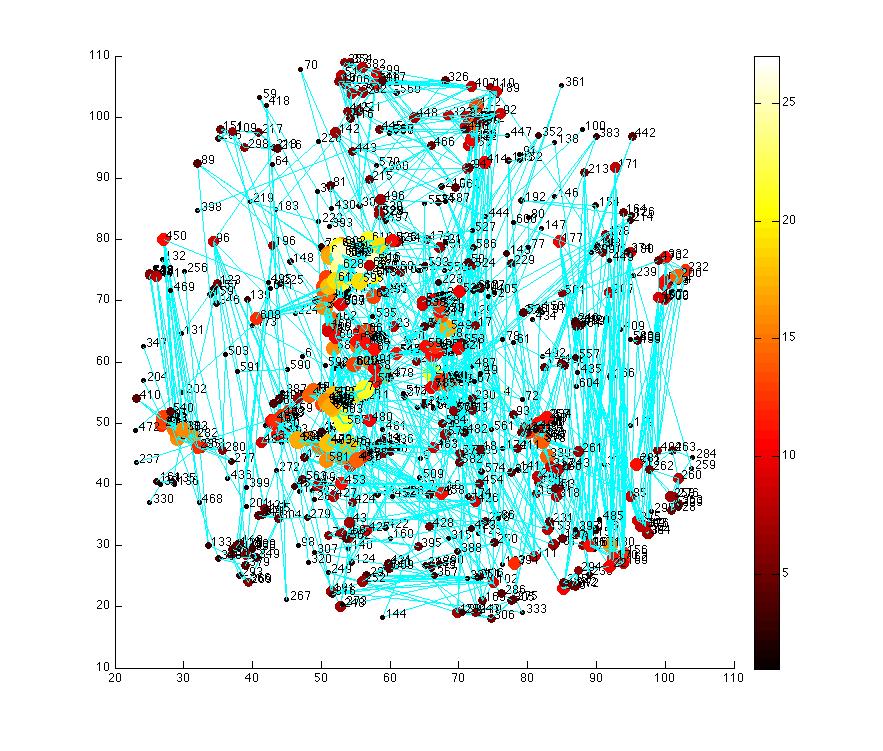
Figure 3. 3D structural brain network showing the node degree.
References
April
22,
2010
- Chung, M.K. Adluru, N. Dalton, K. M., Alexander, A.L.,
Davidson,
R.J. 2010. Characterization
of
structural
connectivity
in autism using graph networks with DTI.
16th Annual Meeting of the Organization for Human Brain Mapping.
938.
- Chung, M.K. Adluru, N. Dalton, K. M., Alexander, A.L.,
Davidson,
R.J. 2011. Scalable
brain network construction on white matter fibers", Proc.
SPIE 7962, 79624G; doi:10.1117/12.874245
- Adluru, N., Chung, M.K., Dalton, K.M., Alexander, A.L.,
Davidson,
R.J. 2010. Characterizing
brain
connectivity using ε-radial nodes: application for classifying
autism. MICCAI workshop on Computational Diffusion MRI.
- Kim, S.-G., Chung, M.K., Hanson, J.L., Avants, B.B., Gee,
J.C.,
Davidson, R.J., Pollak, S.D. 2011. Structural
connectivity
via the tensor-based morphometry. IEEE International
Symposium on Biomedical Imaging (ISBI).


