Description
Diffusion smoothing based on the finite element method (FEM) is introduced in Chung et al (2001). The following self-contained package (diffusion_smooth.zip) perform diffusion smoothing. Simply run DEMO.diffusion.m line by line. You should be able to generate Figure 1. The diffusion_smooth.m routine requires FEM.m that computes A and C matrices associated with the finite element discritization of the given surface mesh (Chung & Taylor, 2004).Instead of solving heat diffusion using FEM, it is possible to solve it as a series expansion involving the heat kernel (Seo et al. 2010, Seo & Chung, 2011). Heat kernel smoothing approach is more stable and robust. This is the approach I strongly recommend to use to smooth surface data and surface itself. The code for heat kernel smoothing is given in here.
Recently we developed the fast polynomial
approximation (Huang
et al. 2019, Huang et al., 2020) in
performing heat kernel convolution. The code for
polynomial approximation is given here.
The method is likely to be the fastest possible
diffusion solver on manifolds.
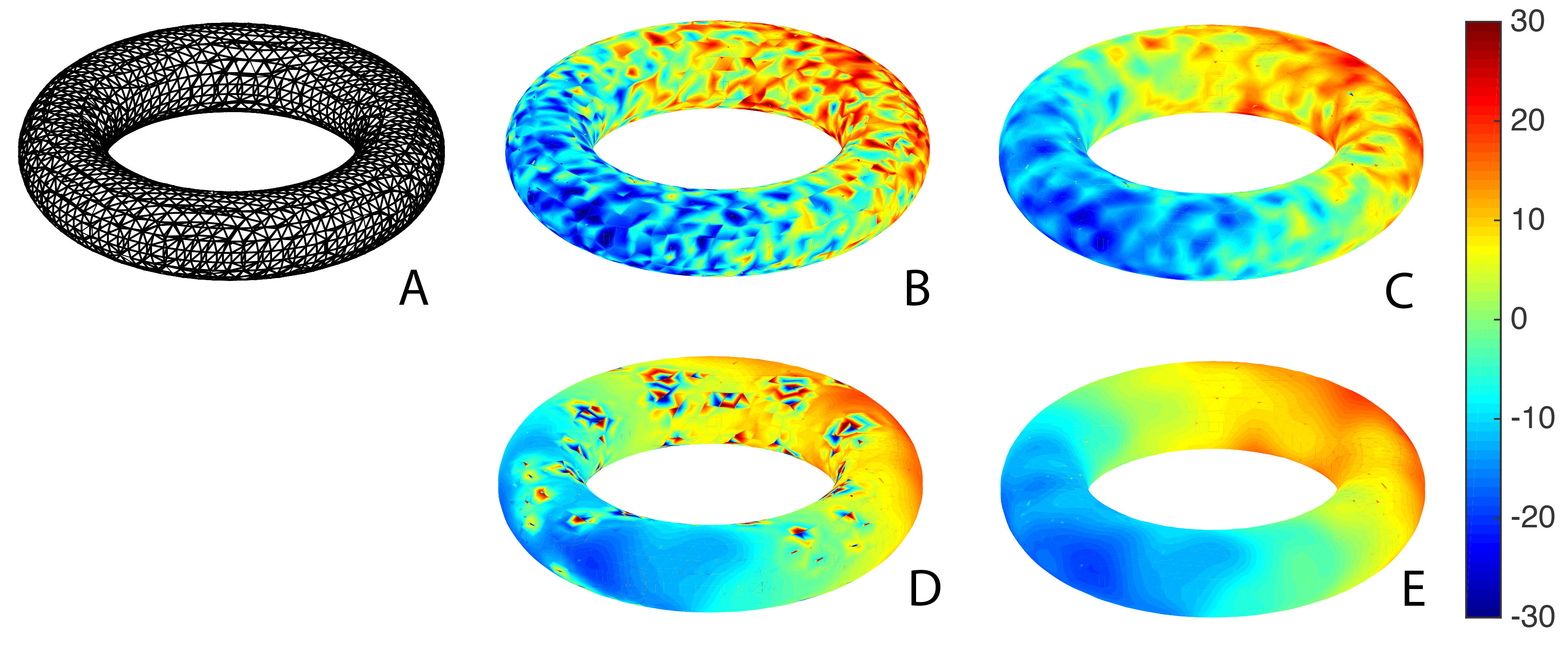
Figure 1. (A) Triangle mesh of a torus. The isosruface algorithm is used to construct the mesh. (B) Simulated data with random noise (C) Diffusion smoothing with sigma=0.1 and 100 iterations (D) Diffusion smoothing with sigma=1 and 100 iterations. The step size 1/100 is too big to converge. (E) Diffusion smoothing with sigma=1 and 2000 iterations.The step size 1/2000 is small enough for convergence.
References
[1] Chung, M.K. 2001. Statistical
Morphometry in Neuroanatomy, PhD Thesis,
McGill University.[2] Chung, M.K., Taylor, J. 2004. Diffusion Smoothing on Brain Surface via Finite Element Method, IEEE International Symposium on Biomedical Imaging (ISBI). 562.
[3] Seo, S., Chung, M.K., Vorperian, H. K. 2010. Heat kernel smoothing using Laplace-Beltrami eigenfunctions. 13th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI). Lecture Notes in Computer Science (LNCS). 6363:505-512.
[4] Seo, S., Chung, M.K. 2011. Laplace-Beltrami eigenfunction expansion of cortical manifolds. IEEE International Symposium on Biomedical Imaging (ISBI).
[5] Huang, S.-G., Lyu, I., Qiu, A., Chung, M.K. 2019. Fast polynomial approximation to heat diffusion in manifolds, Medical Image Computing and Computer Assisted Intervention (MICCAI) 11767:48-56. MATLAB
[6] Huang, S.-G., Lyu, I., Qiu, A., Chung, M.K. 2020. Fast polynomial approximation of heat kernel convolution on manifolds and its application to brain sulcal and gyral graph pattern analysis, IEEE Transactions on Medical Imaging 39:2201-2212 MATLAB