Description
June 3, 2013, April, 29, 2019The following processed dataset and MATLAB codes are used in papers [1, 2, 3]. Using the maltreated children's MRI and DTI data, we will show how to construct the Betti plots from weighted brain graphs. The Betti plots are the basic data visualization and quantification technique in persistent homology but statistical inference procedure has been lacking in the field. he Jackknife based resampling technique is used to compute the p-values here [1, 2, 3] but the exact topological inference procedure [7, 8] is also available.
The codes have been tested under a Macbook pro laptop with 16 GB memory and MATLAB 2009b. The matlab codes below is given jacobian.m. Simply run through the codes line by line. MRI data is given in jacobian.mat. The whole package (codes, references, data) is zippped as jacobian-v2.zip. If you use the codes or data in this page, please reference [1] or [2]. The old version is zipped as jacobian-v1.zip.
3D Graph/Network Visualization
May 14, 2013Matlab binary file jacobian.mat contains various network data used in [1, 2]. It contains the following variables.
jacobian: 54 (# of subject) x 18881 (# of vertices) matrix of Jacobian determinants obtained from MRI
FA : 54 (# of subject) x 18881 (# of vertices) matrix of fractional anisotropy (FA) obtained from DTI.
surf : White matter surface template in MATLAB surface mesh format with 18881 mesh vertices
nodes : 548 Node positions uniformly subsampled from 18881 mesh vertices.
age : Ages of subjects in year
group : Categorical variable indicating if a subject is normal (0) or post institutionalized (PI) children 1.
There are total 31 normal controls and 23 PI.
gender : Categorical variable indicating if a subject is female (0) or male 1
Variable jacobian is the Jacobian determinant of deforming a white matter template to 54 individual surfaces. It is sampled at 18881 mesh vertices. Variable FA is fractional anisotropy obtained from DTI. In this page, we will use jacobian to demonstrate various parts of the codes. But the method can be easily applicable to FA as well.
load jacobian.mat
ind=mesh_commonvertex(surf, nodes);
surfJJ= jacobian(:,ind);
18881 nodes are too large to handle so we subsample the Jacobian determinant at 18881 nodes to 548 nodes using mesh_commonvertex.m, which basically finds the common mesh vertices in the surf mesh using nodes coordinates. This results in the variable surfJJ, which is 54 (# of subjects) x 548 (# of nodes) matrix. We separate the data into two groups indicated by _pi (maltreated) and _co (controls). Then Pearson correlation across nodes are computed as
X=surfJJ(find(group),:);
corr_pi= corrcoef(X);
X=surfJJ(find(~group),:);
corr_co= corrcoef(X);
The correlation matrices of PI and controls are then computed as corr_pi and corr_co respectively. The size of the correlation matrices are 548 x 548 and this is expected to be symmetric but may not be positive definite. The sparse network model in [1] and [2] can be used to make the correlation matrices positive definite. The entries of the correlation matrices give the edge wights in the network model.
To display the networks in 3D, we need the outline of the brain, which is obtained from the template. The white matter surface template is constructed by thresholding the fractional anisotropy (FA) values of the template and stored as variable surf.
figure;
figure_patch(surf, [0.3 0.3 0.3],0.2);
On top of the brain surface, we display 548 network nodes as 3D spheres using
landmarks_nodelabel:
coord = nodes.vertices;
nodevalue = sum(corr_co,1);
landmarks_nodelabel(coord, 3, nodevalue,[])
view([90 90]); camlight;
Subsequently, the stremtube representation is used to display the edges between nodes as 3D tubes. The correlation matrix corr_co above the thresholded at 0.7 is displayed in Figure 1.
landmarks_tubes(corr_co, coord, 0.7);
view([90 90]); camlight;
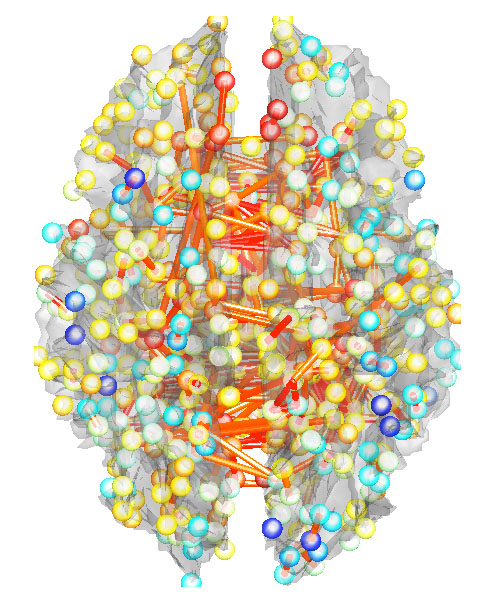
Figure 1.
Streamtube representation of brain networks.
Edges and nodes can be colored differently using
the above tools. If you want your own custom
colormap, you need to modify few lines inside landmarks_nodelabel
and landmarks_tubes
Betti Plots and Jackknife Resampling
May 15, 2013The Betti plot displays Betti numbers (mostly the 0-th Betti number) over the threshold of network edges. The 0-th Betti plot on 1- correlation is constructed by identifying the minimum spanning tree via the Kruskal's algorithm in PHbarcode.m. See [4] for the details on the algorithm. PHbarcode.m inputs the connectivity matrix and outputs the sequence of increasing filtration values that increases the number of components. The Betti plot is then constructed by simply plotting the number of connected components over the increasing filtration value.
figure;
dco=PHbarcode(1-corr_co);
plot([1; 1-dco'], [548:-1:1], '-k');
dpi=PHbarcode(1-corr_pi);
hold on; plot([1; 1-dpi'], [548:-1:1], '--r');
Statistical inference can be done by Jackknife resampling [2]. For 23 PI subject, we remove one subject at a time (leave-one-out scheme) and compute the correlation using only 22 PI subjects. This process is repeated for all 23 subjects and total 23 correlations are generated into MSTpi. MSTpi(:,i)is then the Jackknife resample of the i-th subject.
n1= 23;
n2= 31;
MSTpi=zeros(547,n1);
MSTco=zeros(547,n2);
X=surfJJ(find(group),:);
for i=1:n1
Xi= X;
Xi(i,:)=[];
corr_pi= corrcoef(Xi);
MSTpi(:,i) = PHbarcode(1-abs(corr_pi));
end;
Y=surfJJ(find(~group),:);
for i=1:n2
Yi= Y;
Yi(i,:)=[];
corr_co= corrcoef(Yi);
MSTco(:,i) = PHbarcode(1-abs(corr_co));
end;
MSTpi produces Jackknife resamples in 547 (# of filtrations) x 23 (# of subjects) matrix. The resulting Jackknife resampled barcodes are displayed in Figure 2.
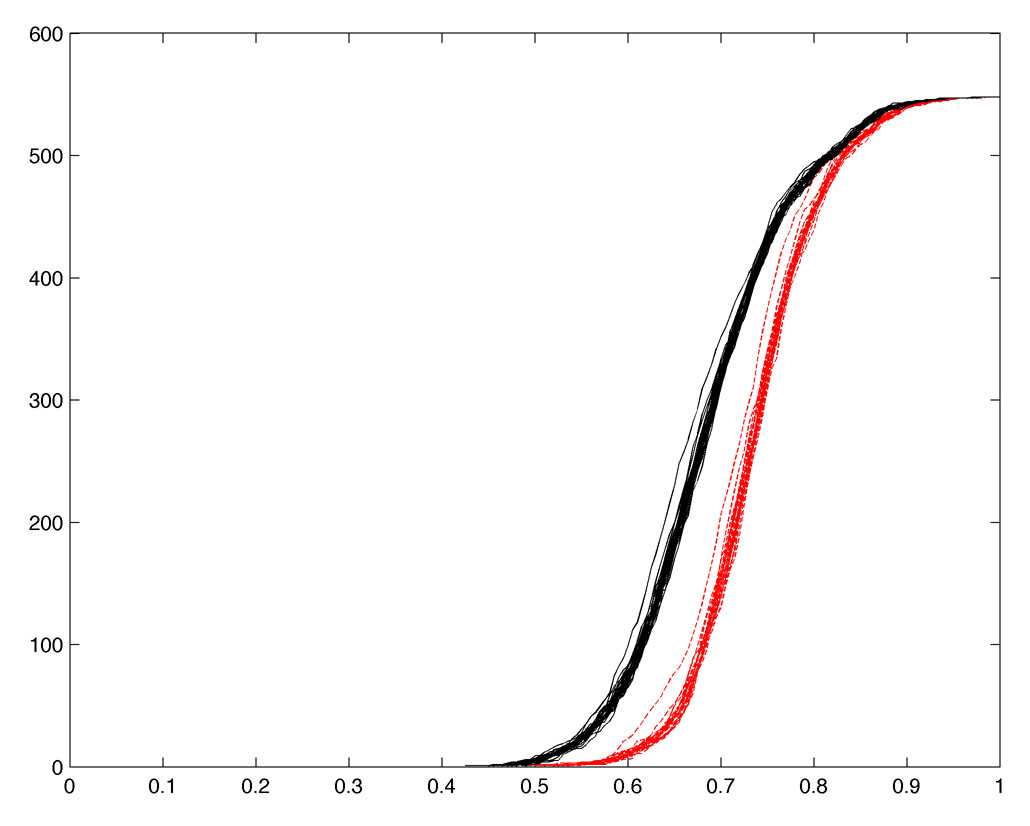
Figure 2. The resulting Jackknife resampled Betti plots are displayed. Black curves are for normal controls and red curves are for maltreated children.
Statistical Inference on Barcodes
May 15, 2013For the statistical inference, we may use Komogorov-Smirnov (KS) like test statistic. In constructing the Betti plot, the horizontal axis (filtration values) is irregularly gridded while the vertical axis (number of connected components) is regularly gridded. To use KS-test easily, the barcodes needs to interpolated in such a way that the horizontal axis is regularly gridded. This is done using by fitting the Betti plot via linear interpolation at regular interval (Figure 3). The regriding on a single barcode is done as follows.
dco=PHbarcode(1-corr_co);
x=[1 1-dco]';
Y=[548:-1:1]';
figure; plot(x,Y, '.k');
xgrid=[0:0.005:1]';
ygrid = interp1(x,Y,xgrid, 'nearest');
hold on; plot(xgrid, ygrid, '+r')
legend('barcode', 'interpolation')
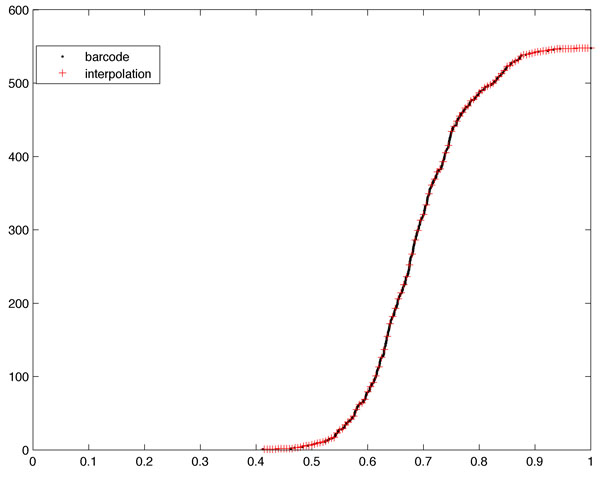
Figure 3. The barcode needs to be resampled at regular grids [0:0.005:1] for the subsequent statistical analysis.
The regriding on Jackknife resampled Betti plots is done as follows.
figure
INTpi=[]
INTco=[]
xgrid=[0:0.005:1]';
Y=[548:-1:1]';
for i=1:n1
dco=MSTpi(:,i)';
x=[1 1-dco];
INTpi(:,i) = interp1(x,Y,xgrid, 'nearest');
hold on; plot(xgrid, INTpi(:,i) ,'r')
end
for i=1:n2
dco=MSTco(:,i)';
x=[1 1-dco];
INTco(:,i) = interp1(x,Y,xgrid, 'nearest');
hold on; plot(xgrid, INTco(:,i),'k')
end
Then we compute the maximum difference between the Betti plots from two groups. This is similar to the KS-test statistic. Under the null hypothesis of no group difference, this difference should be close to zero. The deviation of the difference from zero determine statistical significance. The between-group KS-distance between the Jackknife resamples is computed and stored in variable d:
d=[];
for i=1:n1
for j=1:n2
Mpi=INTpi(:,i);
Mco=INTco(:,j);
diff=max(abs(Mpi-Mco));
d=[d diff];
end
end;
The within-group KS-distance for each group is computed and stored in variable e:
e=[];
for i=1:n1
for j=1:n1
Mpi1=INTpi(:,i);
Mpi2=INTpi(:,j);
diff=max(abs(Mpi1-Mpi2));
if i~=j
e=[e diff];
end;
end
end;
for i=1:n2
for j=1:n2
Mco1=INTco(:,i);
Mco2=INTco(:,j);
diff=max(abs(Mco1-Mco2));
if i~=j
e=[e diff];
end;
end
end;
figure; hist(e,30)
hold on; hist(d, 30)
Figure 4 shows the histogram of within-group (left cluster) and between-group (right cluster) KS-distances. This shows there is really signal between the groups that is far larger than within-group variability can explain. Note that this p-value is multiple comparisons corrected over filtration values between 0 and 1.
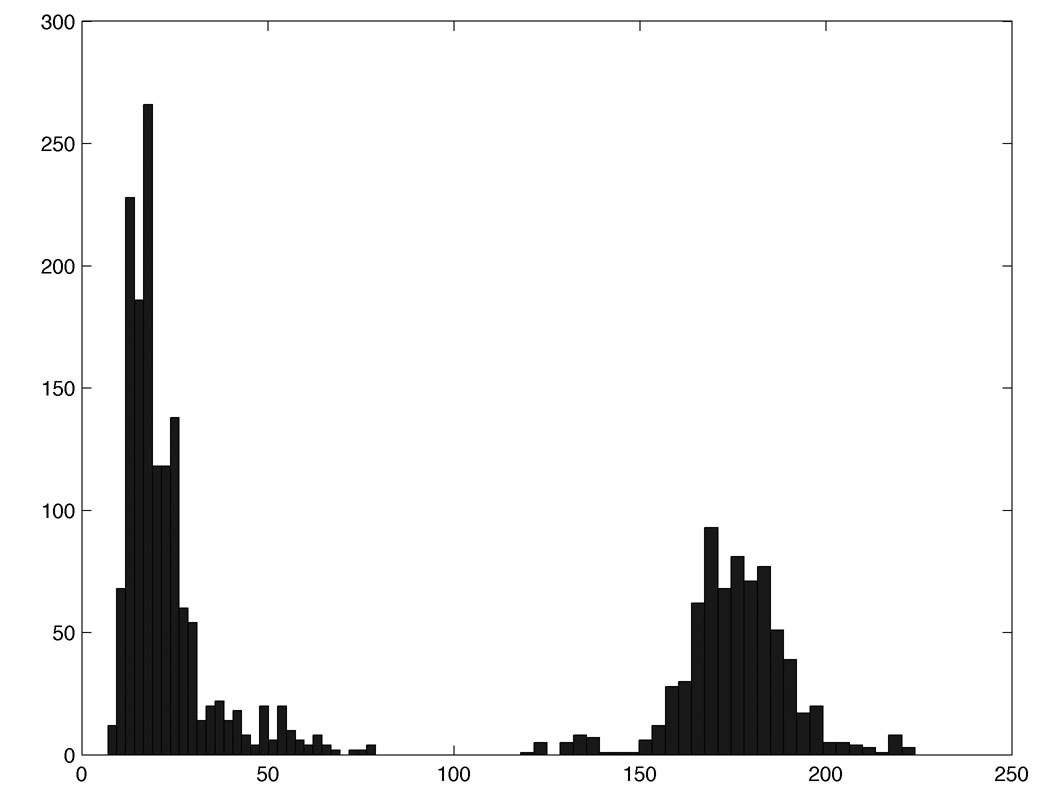
Figure 4. The histogram of within-group (left cluster0 and between-group (right cluster) KS-distances. Whatever test procedures you use, the group difference is highly significant (p-value < 0.001).
Reference
[1] Chung, M.K., Hanson, J.L., Ye, J., Davidson,
R.J. Pollak, S.D. 2015 Persistent
homology in sparse regression and its
application to brain morphometry. IEEE
Transactions on Medical Imaging,
34:1928-1939[2] Chung, M.K., Hanson, J.L., Lee, H., Adluru, N., Alexander1, A.L., Davidson, A.L., Pollak, S.D. 2013. Persistent homological sparse network approach to detecting white matter abnormality in maltreated children: MRI and DTI multimodal study, 16th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI). Lecture Notes in Computer Science (LNCS) 8149:300-307
[3] Chung, M.K., Lee, H., Arnold, A. 2012. Persistent homological structures in compressed sensing and sparse likelihood, NIPS Workshop on Algebraic Topology and Machine Learning.
[4] Lee, H., Kang, H.K., Chung, M.K., Kim, B.-N., Lee, D.S. 2012. Persistent brain network homology from the perspective of dendrogram, IEEE Transactions on Medical Imaging. 31:2267-2277
[5] Lee, H., Chung, M.K., Kang, H., Kim, B.-N., Lee, D.S. 2011. Computing the shape of brain network using graph filtration and Gromov-Haudorff metric. 14th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI). Lecture Notes in Computer Science (LNCS). 6892:302-309
Pachauri, D., Hinrichs, C., Chung, M.K., Johnson, S.C., Singh, V. and ADNI. 2011. Topology-based kernels with application to inference problems in Alzheimer's disease. IEEE Transactions on Medical Imaging. 30:1760-1770
[6] Chung, M.K., Bubenik, P., Kim, P.T. 2009. Persistence diagrams of cortical surface data. Information Processing in Medical Imaging (IPMI). Lecture Notes in Computer Science (LNCS). 5636:386-397
Chung, M.K., Singh, V., Kim, P.T., Dalton, K.M., Davidson, R.J. 2009. Topological characterization of signal in brain images using the min-max diagram. 12th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI). Lecture Notes in Computer Science (LNCS). 5762:158-166
[7] Chung, M.K., Vilalta, V.G., Lee, H., Rathouz, P.J., Lahey, B.B., Zald, D.H. 2017 Exact topological inference for paired brain networks via persistent homology. Information Processing in Medical Imaging (IPMI). 10265:299-310. MATLAB. Extended version: arXiv:1509.04771
[8] Chung, M.K., Luo, Z., Leow, A.D., Alexander, A.L., Richard, D.J., Goldsmith, H.H. 2018 Exact Combinatorial Inference for Brain Images, Medical Image Computing and Computer Assisted Intervention (MICCAI), 11070:629-637